Robust Control Toolbox
Robust Control Toolbox provides functions and blocks for analyzing and tuning control systems to ensure performance and robustness against plant uncertainty. It allows you to create uncertain models by combining nominal dynamics with uncertain elements, like parameters or unmodeled dynamics. The toolbox helps analyze the impact of uncertainty on performance and identify worst-case scenarios. H-infinity and mu-synthesis techniques are used to design controllers that maximize robust stability and performance.
The toolbox integrates robust tuning with the Control System Toolbox, enabling decentralized control with multiple tunable blocks across feedback loops. It optimizes performance for the nominal plant while maintaining a minimum performance level across the entire uncertainty range.

Modeling Plant Uncertainty
Create detailed uncertain models by combining nominal dynamics with uncertain elements, using state-space or frequency response representations.
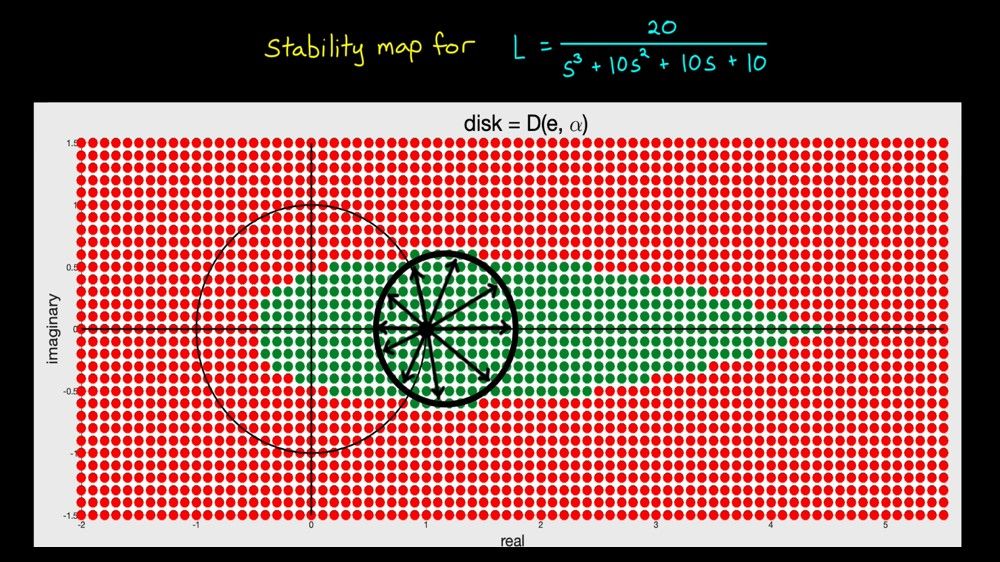
Stability Analysis Using Disk Margins
Assess how uncertainty impacts stability and performance using disk-based gain and phase margins in SISO and MIMO loops.

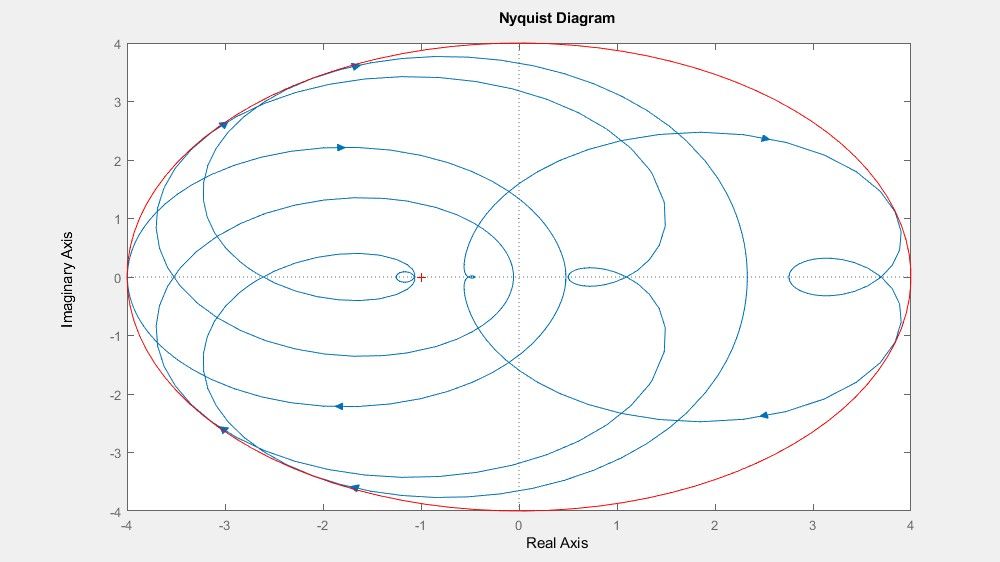
Robustness and Worst-Case Analysis
Compute worst-case performance bounds and robustness margins without random sampling to assess stability and performance tolerance to parameter variations.
Monte Carlo Analysis
Generate random samples of uncertain systems and visualize their impact on time and frequency responses.

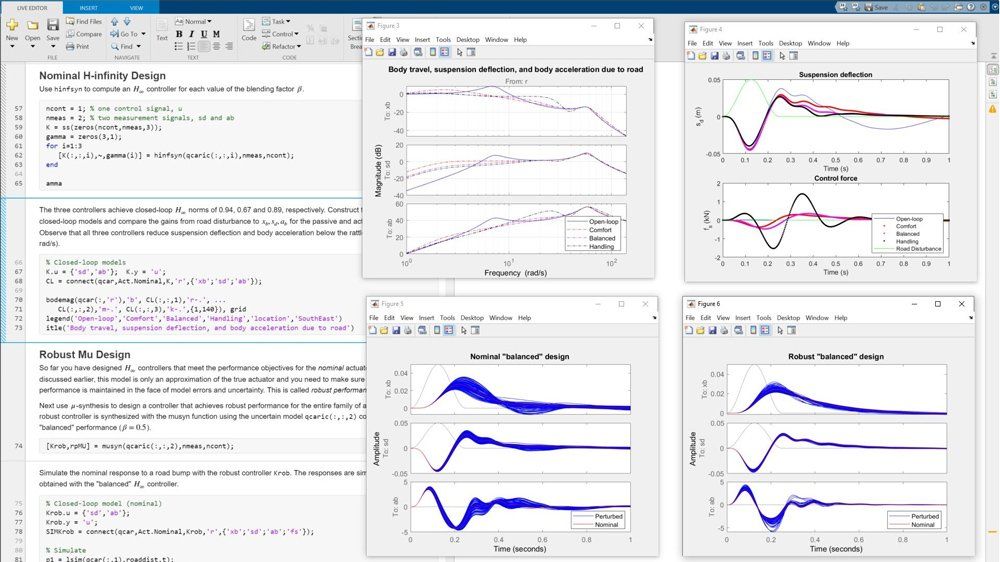
H-Infinity and Mu Synthesis
Design robust MIMO controllers using H-infinity and mu synthesis. Optimize fixed-structure H-infinity performance and automate loop shaping with mixed-sensitivity or Glover-McFarlane methods.
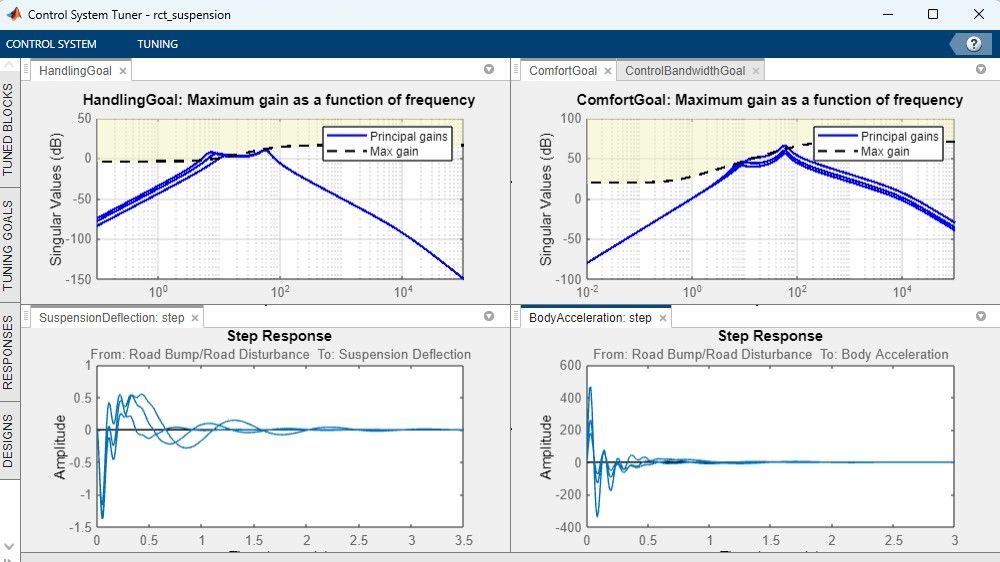
Robust Controller Tuning
Automatically tune control systems for tracking, rejection, and stability using Control System Tuner or systune command, ensuring robust performance under parameter variations.
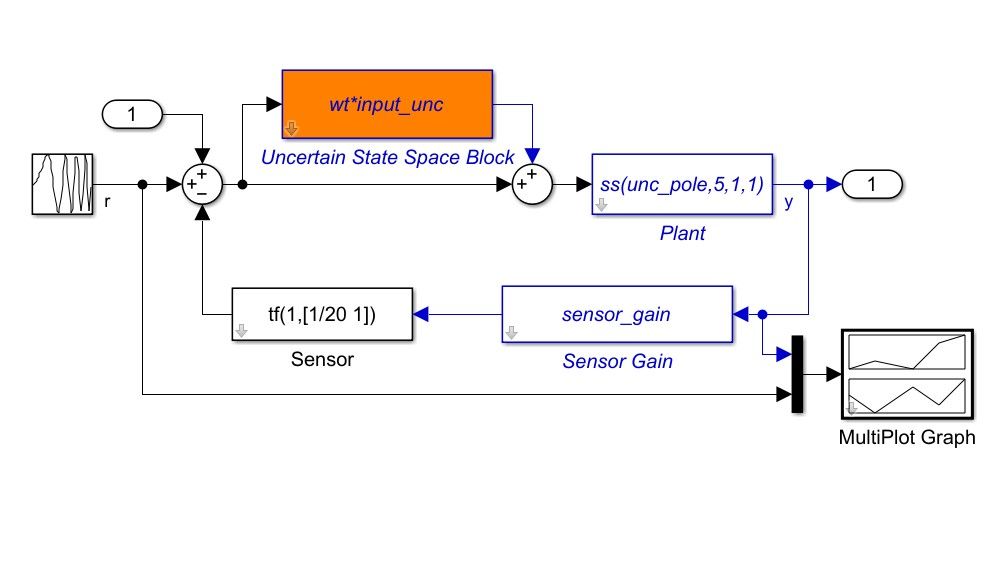
Robust Control Design in Simulink
Represent uncertain elements in a Simulink model and linearize it to analyze the impact of uncertainty on the system. Perform automatic controller tuning of the uncertain system within Simulink.
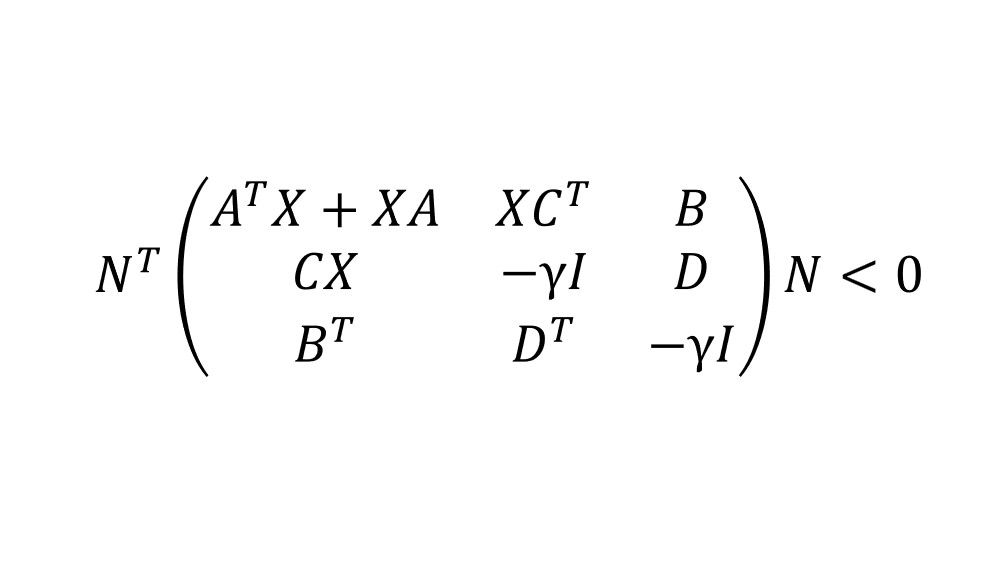
Linear Matrix Inequalities
Specify and solve general linear matrix inequality (LMI) problems using Robust Control Toolbox. It provides LMI solvers for feasibility, cost minimization, and generalized eigenvalue minimization.
Reference Applications
Use reference examples for aerospace, power electronics, and automotive applications to synthesize and tune fixed-structure controllers in MATLAB and Simulink for plant models with uncertainty.

